3D6 = 9
On tire 3 dés et on veut faire 9, on a donc :
\[ \begin{aligned} & dé_1 + dé_2 + dé_3 = 9 \quad && 1 \le dé \le 6 \quad && dé \ge 1 \\ & && && \orange{dé \ge 0} && \quad \Leftarrow \text{ mais c'est ça qu'on voudrait}\\ & o_1 + o_2 + o_3 = 6 && 0 \le o \le 5 \quad && o \ge 0 && \quad \Leftarrow \quad o = dé - 1 \\[1em] \end{aligned} \]On peut alors poser :
3D6 = 15
3 méthodes
- Hardcore
- Facile
- Faussement simple
Hardcore
On tire 3 dés et on veut faire 15, on a donc :
\[ \begin{aligned} & dé_1 + dé_2 + dé_3 = 15 \quad && 1 \le dé \le 6 \quad && dé \ge 1 \\ & && && \orange{dé \ge 0} && \quad \Leftarrow \text{ mais c'est ça qu'on voudrait} \\ & o_1 + o_2 + o_3 = 12 && 0 \le o \le 5 \quad && o \ge 0 && \quad \Leftarrow \quad o = dé - 1 \\[1em] \end{aligned} \]On peut poser :
Mais problème : y a des solutions comme 1 + 1 + 12 et ça existe pas comme face de dé, 12...
On peut dresser la liste des solutions de manières ensembliste :
 =
=
 -
-
 -
-
 -
-
 +
+
 +
+
 +
+
 -
-
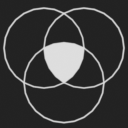
 est l'ensemble de toutes les solutions (incluant les solutions impossibles comme 1 + 1 + 12)
et dont le cardinal précédemment calculé vaut 91.
est l'ensemble de toutes les solutions (incluant les solutions impossibles comme 1 + 1 + 12)
et dont le cardinal précédemment calculé vaut 91.
 est l'ensemble des solutions possibles (sans dés dont une face vaut plus que 6).
est l'ensemble des solutions possibles (sans dés dont une face vaut plus que 6).





 sont les ensembles de solutions avec au moins 2 dés qui valent plus que 6.
sont les ensembles de solutions avec au moins 2 dés qui valent plus que 6.
 est l'ensemble avec les solutions où les 3 dés valent plus que 6. Pour ce dernier, on sait
qu'il est vide car on aurait un résultat plus grand que 15 et on est dans un sous-ensemble
de solutions où la somme vaut 15.
est l'ensemble avec les solutions où les 3 dés valent plus que 6. Pour ce dernier, on sait
qu'il est vide car on aurait un résultat plus grand que 15 et on est dans un sous-ensemble
de solutions où la somme vaut 15.
Calculer le cardinal des 3 premiers ensembles A :
On peut poser :
Calculer le cardinal des 3 ensembles suivants :
On peut poser :
Facile
Il n'y a que ces 3 manières d'obtenir 15 avec 3D6:- 6 + 6 + 3, les permutations donnent 3 arrangements
- 6 + 5 + 4, les permutations donnent 6 arrangements
- 5 + 5 + 5, un seul arrangement
Faussement simple
(car on tombe vite dans un piège ou deux...)
L'idée est de voir qu'il y a autant de chances
de faire 15 que 6.
Comment ce fait-ce ?
Avec 2D6, c'est plus probable de faire 7
(valeur médiane) que 12 ou 2.
Et les chances de faire 12 ou 2 sont les mêmes.
Par extrapolation : la probabilité de 3 = probabilité de 11,
p de 4 = p de 10, etc.
On peut dresser le tableau :
2 3 4 5 6 7 8 9 10 11 12
De la même manière, pour 3D6 on a :
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 16 17 18
probabilité de 15 = probabilité de 6
car à la même distance du centre
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 16 17 18
Donc on va calculer la probabilité pour 6 vu que c'est
la même que pour 15 :
Bonus : probabilité
5 koalas 3 éléphants
Les 4 koalas sont allés chercher des fruits pour en donner un à chacun des 3 éléphants.
Chacun des koala a une seule sorte de fruit en une quantité qui lui est propre.
La répartition est la suivante :
| koala | fruit(s) |
|---|---|
| Amandine | 5 bananes |
| Thor | 3 cerise |
| Nikita | 1 orange |
| Will Smith | 1 tomate |
Note :
Amandine a 5 bananes, mais elle ne pourra jamais en donner plus que 3,
vu qu'il y a 3 éléphants et que chacun n'aura droit qu'à un seul fruit.
De manière générale : on plafonne les éléments du vecteur à \( e \).
Donc \( \{ 5,3,1,1 \} \) devient \( \{ 3,3,1,1 \} \)
La formule est \[ \sum_{\substack{ x_1 + x_2 + x_3 + x_4 ~=~ 3 \\[0.5em] 0 ~\leq~ x_i ~\leq~ o_i }} \frac{3!}{\prod_{i=1}^4 x_i!} \quad;\quad \mathbf{o} = \{ 3,3,1,1 \} \quad;\quad e = 3 \]
On cherche les types partitions ;
les manières de partitionner le don de
3 fruits par les 4 koalas.
Il peut être trouvé avec la formule des
partitions avec le plus grand nombre du
vecteur
( \( p(o_{max}) \), ici \( p(3) = 3 \),
mais c'est vite des formules compliquées).
Ici on les pose (les trois) à la main.
| Types \[ p(3) = 3 \] | Un koala donne ses trois fruits : \[ 3,0,0,0 \] | Un koala donne deux fruits et un autre un fruit : \[ 2,1,0,0 \] | Trois koalas donnent un fruit chacun : \[ 1,1,1,0 \] |
|---|---|---|---|
| Combinaisons possibles \[ 20 \] Combinaisons valides \[ \text{Coeff}(\{ 3,3,1,1 \}, 3) \\[.5em] = 12 \] | \[ 3,0,0,0 \\[.5em] 0,3,0,0 \gray{ \\[.5em] \sout{0,0,3,0}\\[.5em] \sout{0,0,0,3} } \] | \[ \begin{array}{l} 2,1,0,0 \\[.5em] 2,0,1,0 \\[.5em] 2,0,0,1 \\[1em] 1,2,0,0 \\[.5em] 0,2,1,0 \\[.5em] 0,2,0,1 \\[1em] \end{array} \gray{ \begin{array}{l} \sout{ 1,0,2,0 } \\[.5em] \sout{ 0,1,2,0 } \\[.5em] \sout{ 0,0,2,1 } \\[1em] \sout{ 1,0,0,2 } \\[.5em] \sout{ 0,1,0,2 } \\[.5em] \sout{ 0,0,1,2 } \\[1em] \end{array} } \] | \[ 1,1,1,0 \\[.5em] 1,1,0,1 \\[.5em] 1,0,1,1 \\[.5em] 0,1,1,1 \] |
| Arrangements | \[ 2 \frac{3!}{3!~0!~0!~0!} = 2 \] | \[ 6 \frac{3!}{2!~1!~0!~0!} = 18 \] | \[ 4 \frac{3!}{1!~1!~1!~0!} = 24 \] |
| \[ \sum_{\substack{ x_1 + x_2 + x_3 + x_4 ~=~ 3 \\[0.5em] 0 ~\leq~ x_i ~\leq~ o_i }} \frac{3!}{\prod_{i=1}^4 x_i!} \quad=\quad 2 + 18 + 24 \quad=\quad \underline{\underline{44}} \] | |||
Alors, c'était pas si compliqué. Le plus dur c'est surtout de faire en sorte que les koalas ne manges pas les fruits.
Prendre 4 parmi 3x3
Combien y a-t-il d'arrangements possibles de 4 lettres parmi AAABBBCCC ?
Variables (3 A, 3 B et 3 C) :
Formule :
Estimation de la complexité de l'exercice :
Donc 15 termes (maximum) à additionner : faisable
Enumération / définition des groupes de termes :
Formule finale :
Cadenas mode hard
La formule la plus simple c'est évidemment \( 10^3 (= 1000) \),
et on va la garder sous le coude pour vérifier à la fin si on a bien le même résultat.
Mais donc ici on est en mode hard, c'est-à-dire qu'on va utiliser
\[ \begin{aligned}
& \sum_{
\begin{matrix}
x_1 + x_2 + ... x_k = e \\
0 \leq x_i \leq o_i
\end{matrix}
}
~~~
\frac{ e! }{
\prod_{i=1}^k x_i!
}
\end{aligned} \]
et il faut bien poser le problème...
A votre avis, quelles sont les bonnes variables à poser ?
\[ \begin{aligned} & 1. && \mathbf{o} = \{ 10,10,10 \} ; && e = 3 \\[1em] & 2. && \mathbf{o} = \{ 3,3,3,3,3,3,3,3,3,3 \} ; && e = 3 \\[1em] & 3. && \mathbf{o} = \{ \infty,\infty,\infty,\infty,\infty,\infty,\infty,\infty,\infty,\infty, \} ; && e = 3 \end{aligned} \]
Pourquoi j'ai posé ces trois-cis ?
La première est une erreur qui (en tout cas chez moi) vient tout de suite de manière intuitive : on a trois chiffres qui chacun peuvent avoir 10 valeurs.
Mais c'est bien la deuxième formule qui est correcte pour exprimer le problème : on a une collection de 30 chiffres répartis en 10 catégories distinctes.
On pourrait (devrait) même prendre la troisième : on a une infinité de chiffres à disposition mais de 10 types différents.
Mais alors pourquoi la 2. et pas la 3. ?
Comment pour l'exerice des koalas : on ne pourra jamais prendre plus que 3 chiffres identiques étant donné qu'on a que trois emplacements à disposition. On va donc "clamper" les valeurs à 3.
Il y a 3 manières (Types) de prendre trois chiffres :
- 3 chiffres identiques
- 2 chiffres identiques et 1 autre
- 3 chiffres différents
La formule donne donc :
\[ \begin{aligned} & 10 \frac{3!}{ 3! \gray{0!0!0!0!0!0!0!0!0!} } + 90 \frac{3!}{ 2! \gray{1!0!0!0!0!0!0!0!0!} } + 120 \frac{3!}{ \gray{1!1!1!0!0!0!0!0!0!0!} } = \\[2em] & 10 \quad+\quad 90 \cdot 3 \quad+\quad 120 \cdot 6 \quad=\quad 10 + 270 + 720 \quad=\quad \underline{\underline{1000}} \end{aligned} \]
By the way, le nombre de combinaisons totales
( \( 220 \) )
es bien donné par la somme des combinaisons
( \( 10 + 90 + 120 \) )
Vérification, prendre 3 parmis 10 avec répétition :
\[
\overline{C}_{3}^{10} ~~=~~
C_{3}^{12} ~~=~~
\frac{12!}{3!9!} ~~=~~
\frac{10 ~ 11 ~ \sout{12} ~ 2}{\sout{3 ~ 2}}
~~=~~
220
\]