Fonctions

Définition

\[ \begin{aligned} & f: && A && \to && B \\ & && x && \mapsto && f(x) \end{aligned} \]
\[ \begin{aligned} & fonction: && domaine && \to && codomaine \\ & && préimage && \mapsto && image \end{aligned} \]
\[ \begin{aligned} & f: && A=Dom(f) && \to && Im(f)=f(A)\subseteq B \\ & && x && \mapsto && f(x) \end{aligned} \]

Composition de fonctions

\[ \begin{aligned} & f(x) = x^2 \\[1em] \end{aligned} \\ \begin{aligned} & f: && \mathbb{R} && \to && \mathbb{R}_+ \\ & && x && \mapsto && f(x) \end{aligned} \]
\[ \begin{aligned} & g(x) = ln(x) \\[1em] \end{aligned} \\ \begin{aligned} & g: && \mathbb{R}_+ && \to && \mathbb{R} \\ & && x && \mapsto && g(x) \end{aligned} \]
\[ \begin{aligned} & (\blue{f} \circ \orange{g})(x) \quad = \quad \blue{f(}\orange{g(}x\orange{)}\blue{)} \\ \end{aligned} \\ \begin{aligned} \\ & \mathbb{R}_+ \orange{\xrightarrow[]{g}} \mathbb{R} \blue{\xrightarrow[]{f}} \mathbb{R}_+ \\[1em] \end{aligned} \\ \begin{aligned} & \blue{f} \circ \orange{g}: && \mathbb{R}_+ && \to && \mathbb{R}_+ \\ & && x && \mapsto && (\blue{f} \circ \orange{g})(x) \end{aligned} \]

Fonctions "inverses"

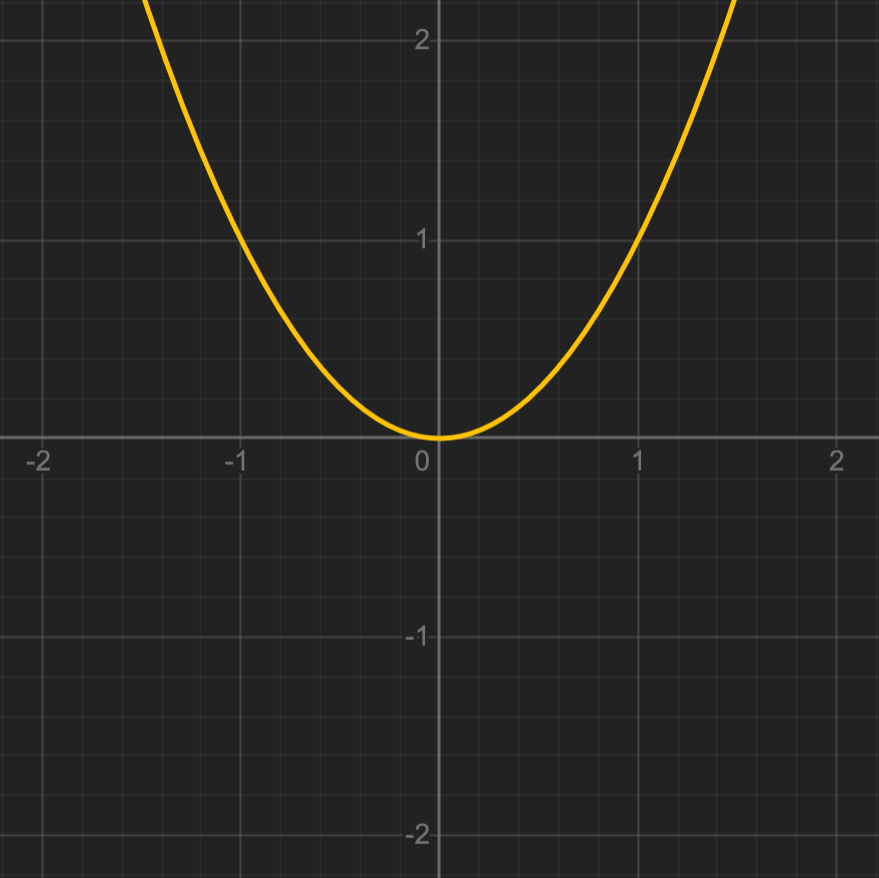
fonction \[ f(x) \] 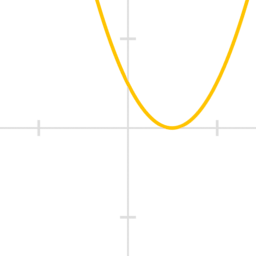\[ x^2-2x+1 \] \[ D(f)=\mathbb{R} \quad;\quad Im(f)=\mathbb{R}_+ \] opposée \[ -f(x) \] 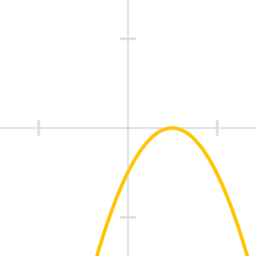\[ -(x^2-2x+1) \] \[ D(-f)=\mathbb{R} \quad;\quad Im(f)=\mathbb{R}_- \]
? \[ f(-x) \] 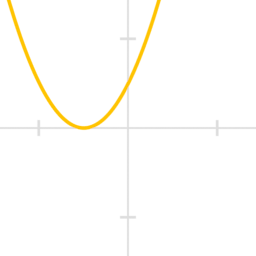\[ (-x)^2-(-2x)+1 \] \[ D(?)=\mathbb{R} \quad;\quad Im(?)=\mathbb{R}_+ \] réciproque ("inverse") \[f^{-1}(x)\] \[ \left\{ \begin{array}{ll} x \ge 0 \quad 1 + \sqrt{x} \\[1em] x \le 0 \quad 1 - \sqrt{x} \end{array} \right. \] \[ \left\{ \begin{array}{ll} D(f^{-1})=\mathbb{R_+} \quad;\quad Im(f^{-1})=[1, \infty[ \\[1em] D(f^{-1})=\mathbb{R_+} \quad;\quad Im(f^{-1})=]-\infty , 1] \end{array} \right. \]

injectif + surjectif = bijectif

\[ f(x) \] Injective
\[ x^2 \]
\[ e^x \]
Surjective
\[ x^3-x \]
\[ x^3 \]

Types de fonctions

\[ f(x) = \] \[ 0 \] \[ 3.7 \] \[ 2x \] \[ 3x + 4 \] \[ x \] \[ e^x \] \[ x^3 -x \] \[ x^3 \]
nulle constante linéraire affine monotone injective surjective bijective