| \[ 0 \] | \[ \frac{\tau}{12 }\] | \[ \frac{\tau}{8} \] | \[ \frac{\tau}{6} \] | \[ \frac{\tau}{4} \] | |
| \[ 0 \] | \[ \frac{\pi}{6}\] | \[ \frac{\pi}{4} \] | \[ \frac{\pi}{3} \] | \[ \frac{\pi}{2} \] | |
| \[ sin \] | \[ \frac{\sqrt{0}}{2} \] | \[ \frac{\sqrt{1}}{2} \] | \[ \frac{\sqrt{2}}{2} \] | \[ \frac{\sqrt{3}}{2} \] | \[ \frac{\sqrt{4}}{2} \] |
| \[ cos \] | \[ \frac{\sqrt{4}}{2} \] | \[ \frac{\sqrt{3}}{2} \] | \[ \frac{\sqrt{2}}{2} \] | \[ \frac{\sqrt{1}}{2} \] | \[ \frac{\sqrt{0}}{2} \] |
| \[ tan \] | \[ 0 \] | \[ \frac{1}{\sqrt{3}} \] | \[ 1 \] | \[ \frac{\sqrt{3}}{1} \] | \[ - \] |
Quotients
\[ \begin{aligned}
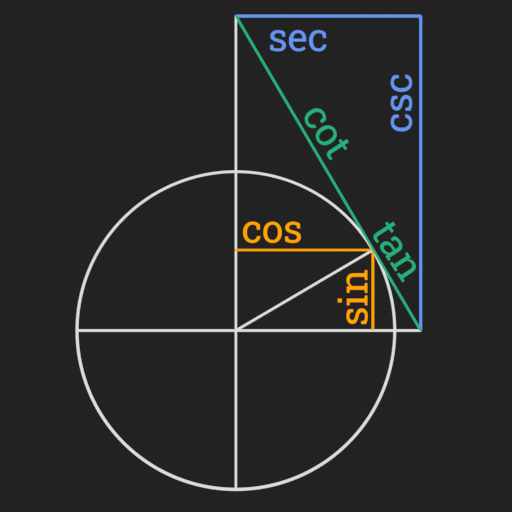
& \orange{\frac{sin}{cos}} = \frac{\green{tan}}{1} = \frac{1}{\green{cot}} =
\blue{\frac{sec}{csc}}
\end{aligned} \]
\[ \begin{aligned}
& \blue{sec} = \frac{1}{\orange{cos}}
\end{aligned} \]
\[ \begin{aligned}
& \blue{csc} = \frac{1}{\orange{sin}}
\end{aligned} \]
Angles
\[ \begin{aligned}
& c^2 = a^2 + b^2 - 2ab\,cos(\theta) \\[1.5em]
& \frac{A}{sin(\alpha)} = \frac{B}{sin(\beta)} = \frac{C}{sin(\gamma)}
\end{aligned} \]
Sommes
\[ \begin{aligned}
& sin(\alpha \green± \beta) = sin(\alpha)cos(\beta) \; \green± \; cos(\alpha)sin(\beta) \\[1.5em]
& \rightarrow \quad sin( 2\alpha) = 2sin(\alpha)cos(\alpha) \\[2.5em]
& cos(\alpha \green± \beta) = cos(\alpha)cos(\beta) \; \red∓ \; sin(\alpha)sin(\beta) \\[1.5em]
& \rightarrow \quad cos(2 \alpha) = cos^2(\alpha) - sin^2(\alpha) \\[2.5em]
& tan(\alpha \green± \beta) = \frac{tan(\alpha) \green± tan(\beta)}{1 \red∓ tan(\alpha)tan(\beta)}
\\[1.5em]
& \rightarrow \quad tan(2\alpha) = \frac{2tan(\alpha)}{1 - tan^2(\alpha)}
\end{aligned} \]
Pythagore
\[ \begin{aligned}
& sin^2(\theta) + cos^2(\theta) = 1 \\[1.5em]
& \blue{co}sec^2(\theta) - \blue{co}tan^2(\theta) = 1
\end{aligned} \]